Função Modular / Função com Módulo - Matemática

Não está entendendo nada de função modular? Veja passo a passo como resolvê-la:


Dada f(x) = |x² + 2x| + 2:

a-) Reescreva a função sem a utilização do símbolo de módulo, e esboce o gráfico de f(x), indicando, domínio, imagem, intercepção com eixos coordenados e vértices.

1ºPasso:

Resolver a equação de segundo grau, que está dentro do módulo, que no caso é x² + 2x:

PS: Para quem não sabe resolver equação de segundo grau, clique aqui.

B² - 4.A.C => 2² - 4 x 1 x 0 => 4 = DELTA
-b ± Raiz quadrada de Δ / 2 . A
-2 ± Raiz quadrada de 4 / 2 x 1
-2 ± 2 / 2

-2 + 2 / 2 => 0
-2 -2 / 2 => -2

Agora com os valores das raízes de 'x' da função que está dentro do módulo, podemos fazer um pequeno esboço:

2ºPasso:

Reescrever a função sem uso do símbolo de módulo:

Você terá que criar 2 funções novas:
A primeira função será exatamente igual, só que sem o módulo -> x² + 2x + 2
A segunda função, única coisa que mudará é o que está dentro do módulo. Você deverá inverter os sinais do que está dentro do módulo -> -x² - 2x + 2.

Agora você terá que criar uma restrição para essas duas funções criadas, a primeira delas tem que obter raízes POSITIVAS e a segunda equação tem que obter raízes NEGATIVAS, fazendo desta forma:

Observe esse esboço e procure uma maneira para X ser positivo e outra maneira para X ser negativo:

Observando o esboço você verá que para X ser positivo o X tem que ser ≤ que -2 e X tem que ser ≥ que 0.

Para X ser negativo o X tem que estar entre -2 e 0, ficando assim: -2


3ºPasso:

Montar o gráfico das duas funções descobertas:

Primeira Função:

x² + 2x + 2
DELTA = 4-4(1)(2) = -4

Utiliza-se as seguintes fórmulas para achar o centro da parábola:

-B/2 x A e -DELTA/4 x A

-2 /2 = -1 4/4 = 1

Então o centro é: (-1,1)

X | Y
------
0 | 2
-2| 2
1 | 5
-3| 5

Segunda Função:

-x² - 2x + 2
DELTA = 4-4(-1)(2)=12

Utiliza-se as seguintes fórmulas para achar o centro da parábola:

-B/2 x A e -DELTA/4 x A

2/-2 = -1 -12/4 x -1 = 3

Então o centro é: (-1,3)

X | Y
------
0 | 2
-1| 2

4ºPasso:

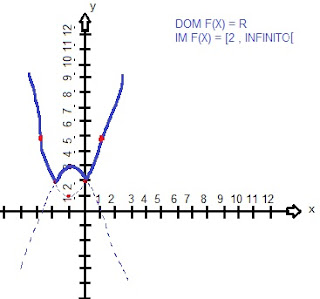
Agora é só montar o gráfico, e apagar o que não se necessita:

Para saber qual parte do gráfico se apaga (TRACEJADO) é com a própria função descoberta:

f(x) = x² + 2x + 2, se x ≥ 0 ou x ≤ -2.
f(x) = - x² - 2x + 2, se -2 < x < 0.

Na primeira função apenas ficará visível onde 'x' for maior e igual que 0 e 'x' for menor e igual a -2, o restante será tracejado.

Na segunda função o que ficará visível é tudo que está entre -2 e 0, o restante será tracejado.